using TDAmapper
import GeometricDatasets as gd
X = gd.sphere(1000, dim = 2);Ball mapper
The Vietoris-Rips complex
Another way to reduce the complexity of a metric space is to approximate it by a simplicial complex. Simplicial complexes are like small building blocks glued together, each of these blocks a small representative of an \(n\)-dimensional space: points, line segments, triangles, tetrahedrons, and so on.
The Vietoris-Rips complex is build as follows: given a metric space \((X, d)\) and an \(\epsilon > 0\), define the following simplicial complex:
\[ VR(X, \epsilon) = \{ [ x_1, \ldots, x_n ] \; d(x_i, x_j) < \epsilon, \forall i, j \} \]
that is: the points of \(X\) are our vertices, and we have an \(n\)-simplex \([x_1, \ldots, x_n]\) whenever the pairwise distance between \(x_1, \ldots, x_n\) is less than \(\epsilon\). This condition is equivalent to ask that
\[ \cap_i B(x_i, \epsilon) \neq \emptyset \]
where \(B(x, \epsilon)\) is the ball of center \(x\) and radius \(\epsilon\).
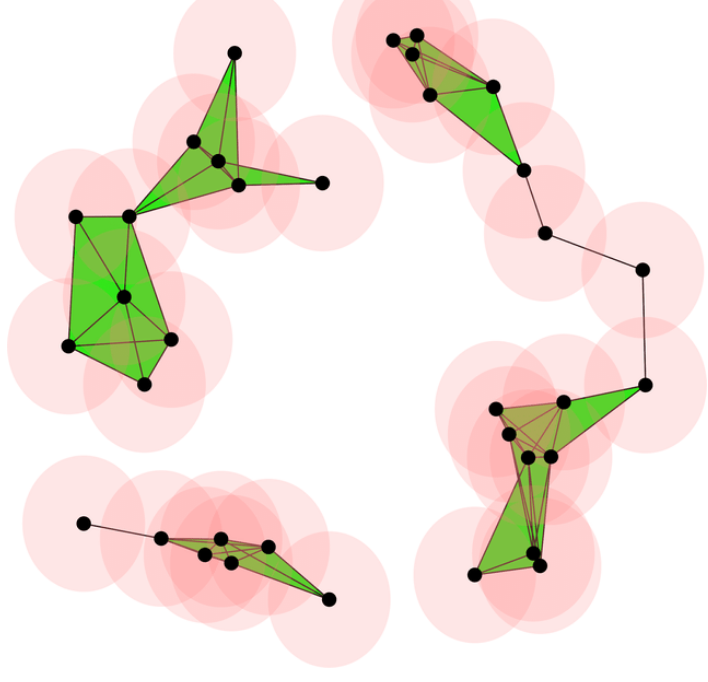
The ball mapper
The ball mapper is clearly inspired by the Vietoris-Rips complex. Given a metric space \((X, d)\) with \(X = \{x_1, \ldots, x_n\}\), select a subset of indexes \(L \subseteq \{1, \ldots, n\}\) and define the ball mapper graph G as follows: the set of vertices of \(G\) is \(L\), and set of edges \(E\) given by
\[ (i, j) \in E \Leftrightarrow B(x_i, \epsilon) \cap B(x_j, \epsilon) \neq \emptyset \]
The ball mapper then can be seen as the 1-skeleton of the Vietoris-Rips, but create using balls whose center can only be the elements indexed by \(L\).
To exemplify, consider a circle
Check that it is indeed a circle:
using CairoMakie
scatter(X)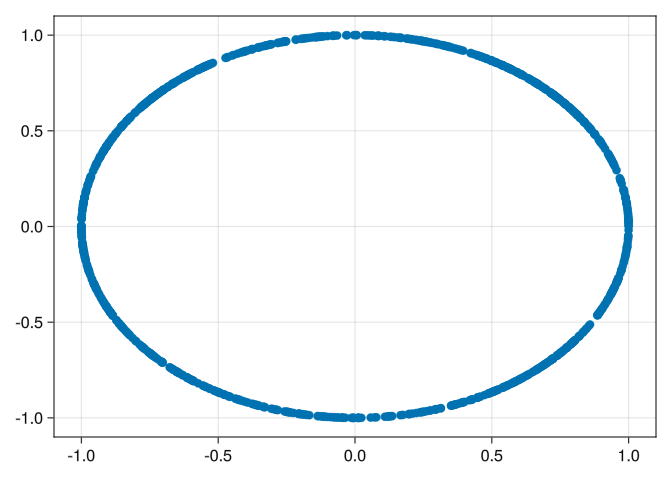
Now take \(L\) as a hundred random points and let’s create the ball mapper of \(X\) with radius \(\epsilon = 0.1\):
L = rand(1:1000, 100)
mp = ball_mapper(X, L, ϵ = 0.5);mapper_plot(mp)
That’s quite a circle!