The Reaven and Miller diabetes dataset

Let’s reproduce the results of […].

Dataset

To load the dataset, we will use a R package that contains it, and then convert it to a Julia DataFrame. You will need a working R installation for that.

using RCall
using TidierData
using TDAmapper

df = R"""
if (require("rrcov") == FALSE) {
    install.packages("rrcov")
}

library(rrcov)
data("diabetes")

diabetes
""" |> rcopy;

┌ Warning: RCall.jl: Carregando pacotes exigidos: rrcov
│ Carregando pacotes exigidos: robustbase
│ Scalable Robust Estimators with High Breakdown Point (version 1.7-4)
│ 
└ @ RCall ~/.julia/packages/RCall/LWzAQ/src/io.jl:172

first(df, 10)

10×6 DataFrame

Row	rw	fpg	glucose	insulin	sspg	group
	Float64	Int64	Int64	Int64	Int64	Cat…
1	0.81	80	356	124	55	normal
2	0.95	97	289	117	76	normal
3	0.94	105	319	143	105	normal
4	1.04	90	356	199	108	normal
5	1.0	90	323	240	143	normal
6	0.76	86	381	157	165	normal
7	0.91	100	350	221	119	normal
8	1.1	85	301	186	105	normal
9	0.99	97	379	142	98	normal
10	0.78	97	296	131	94	normal

Now, let’s extract only the numeric columns

pre_X = @chain df begin
    @select(rw, fpg, glucose, insulin, sspg)
    Matrix    
    end;

and normalize them

function normalize(x)
    dev = std(x)
    if (std(x) ≈ 0) 
        dev = 1
    end

    (x .- mean(x)) ./ dev
end

X = mapslices(normalize, pre_X, dims = 1)' |> Matrix;

Ball mapper

Now we calculate the ball mapper using all nodes, and setting \(\epsilon = 0.5\):

mp = ball_mapper(X, [1:size(X)[2];], ϵ = 0.5);

The resulting graph is the following

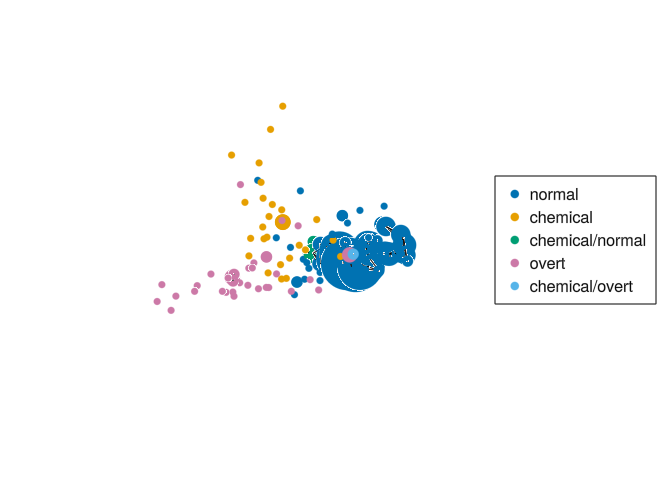
node_values = node_colors(mp, df.group .|> string)
node_positions = layout_mds(mp.CX, dim = 3)

mapper_plot(mp, node_values = node_values, node_positions = node_positions)

We colored each node by the most commom type of diabetes of the points in the node. We can see two branches coming from the center: one going left, with overt type diabetes, and another one going up, with chemical type diabetes.